Part 1: Numpy

Part 1: Numpy#

We have just learned about the logical set-up of a computer and which factors affect the performance of it. Keeping this in mind, we will learn how we can improve the performance of our code in Python.

FYI: To get some more practice in using numpy, do some more exercises which suite your skill level from Nicolas Rougier’s 100 Numpy Exercises.

1. For-Loop vs Vectorized Computation#

The theme of the EuroSciPy Conference 2018 was: “Vectorized is better than an explict loop” But what does this mean?

Example: Calculate the element-wise sum of two lists#

For example:

list1 = [1,2,3]
list2 = [4,5,6]
expected_result = [5,7,9]

E: Create two lists which contain the numbers from 0 to 1000.

E: Caculate the sum of the two lists using a for loop and measure the execution time using the magic command %%timeit

E: Convert the lists to numpy arrays and perform the calculation again using the same code as above. Measure the execution time.

E: Perform the calculation using a numpy ufunc and measure the execution time. Compare the exectuion times of all methods. What do you observe?

Can the logical setup of a computer explain the differences?#

Lists vs Numpy Arrays#

Arrays are better than lists for continous reading of data, because lists usually only store pointers to variables stored in memory, not the variable values themselves. This can lead to bad spatial locality when reading the data, because the data might be spread all over the memory.

What about `np.vectorize`?#

There is a numpy.vectorize() function which seems like it vectorizes your Python code. Execute the code below and compare the results to the previous ones. Is it faster?

def add_values(a, b):
    "Adds a and b"
    return a + b

add_values_vect = np.vectorize(add_values)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[3], line 1
----> 1 add_values_vect = np.vectorize(add_values)

NameError: name 'np' is not defined

%%timeit
add_values_vect(values1, values2)

E: Take a look at the documentation of the numpy.vectorize() fucntion. How does numpy.vectorize() perform the calculation?

Bonus: Write the function above as a lambda function.

Vectorizing your script using Numpy#

Avoid for loops (or even nested for loops) when possible.
Perform calculations on arrays instead of scalars
Use Numpy’s built-in universal functions (ufunc) whenever possible to enable vectorized computation.

Conclusion: Use lists if the elements are of different data type or you do not need to perform any calculations. Otherwise use numpy arrays.

2. Spatial Locality#

Exercise Create a 2-dimensional array with random numbers with 10000 rows and 10000 columns.

By the way: How can you make the function always yields the same random numbers for better reproducibility?

Exercise: Calculate the mean of each row and the mean of each column. Measure how long each of these operations takes. What do you observe?

Looking at the way arrays are stored in pyhsical memory might help us explain this phenomenon.#

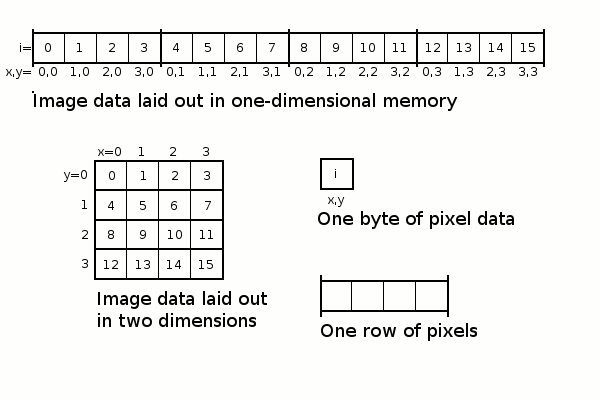
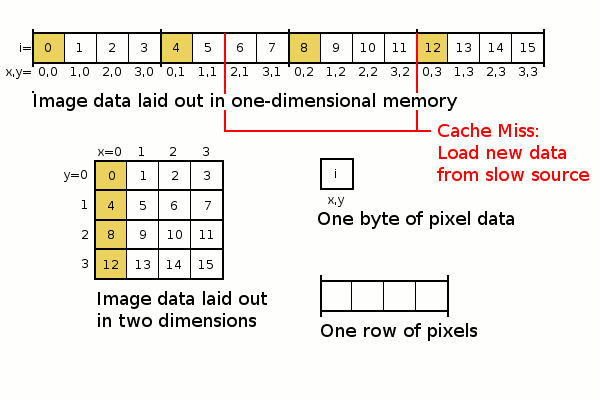
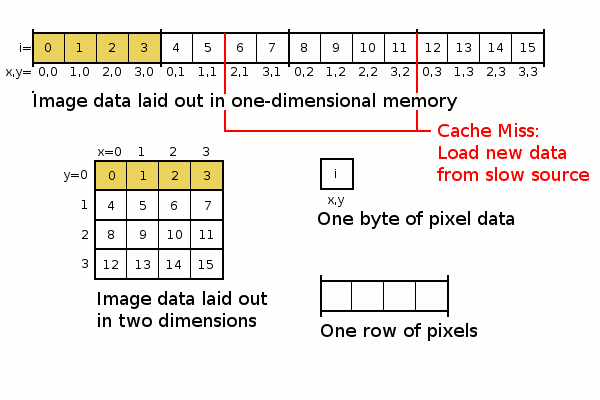
spatial_locality_example1 spatial_locality_example2 spatial_locality_example3

Source: Spatial locality explained

Row and Column Major Order#

By default numpy arrays are stored in C order (row-major), not in F order (column-major). Therefore, calculations along the rows (axis=1) are faster than along the columns (axis=0) for a 2D array. So calculating the mean of each row is faster than the mean of each column if the numpy array is stored as default in C order.

→ SciPy Lectures: C/F order

E: Create a 2-dimensional array of shape 10 and 5 containing the numbers 0 to 49.

E: Convert this 2d array into a 1D array using F order.

4. Bonus: Numpy Strides#

“Strides are the number of bytes to jump-over in the memory in order to get from one item to the next item along each direction/dimension of the array. In other words, it’s the byte-separation between consecutive items for each dimension.” Stack Overflow

–> SciPy Lectures: Strides

E 2.1: Create an array arr with values ranging from 10 to 49 of data type “int8” (8-bit integer).

E: Print the strides of arr.

arr.strides

E: change the data type of arr to 16-bit integer and print the strides again. Why do they change?

E: Reshape the array so that it has 4 rows and 10 columns and print the strides again.

Explanation: To get to the next row you need to jump 10 * 2 bytes (16 bit integer = 2 byte). To get to the next column you need to jump 1 * 2 bytes.

E: What happens to the data in memory when you transpose the array arr3?

Bonus exercise:#

Create an F ordered array with 15 columns and 10 rows with data type 32bit float. Calculate the strides by yourself. Check your result by executing the strides.

Summary#

You should be able now to explain the sentence “vectorized is better than an explicit loop”.
When performing calculations it is good to keep in mind how arrays are stored in memory, since it can influence your processing time.
Most of the time however, NumPy or Python take care of it if you use their built-in functions. So usually you don’t need to worry about this, but if your data gets very big it is good to have this mind.